FÍSICA-MECÂNICA
ENERGIA MECÂNICA
Prof. Alberto Ricardo Präss (alberto@fisica.net)

|
S |
em dúvida nenhuma energia é o termo técnico, originário da Física, mais empregado em nossa vida cotidiana.
Energia é um conceito muito abrangente e, por isso mesmo, muito abstrato e difícil de ser definido com poucas palavras de um modo preciso. Usando apenas a experiência do nosso cotidiano, poderíamos conceituar energia como “algo que é capaz de originar mudanças no mundo”. A queda de uma folha. A correnteza de um rio. A rachadura em uma parede. O vôo de um inseto. A remoção de uma colina. A construção de uma represa. Em todos esses casos, e em uma infinidade de outros que você pode imaginar, a interveniência da energia é um requisito comum.
Muitos livros definem energia como “capacidade de realizar trabalho”. Mas esta é uma definição limitada a uma área restrita: a Mecânica. Um conceito mais completo de energia deve incluir outras áreas (calor, luz, eletricidade, por exemplo). À medida que procuramos abranger áreas da Física no conceito de energia, avolumam-se as dificuldades para se encontrar uma definição concisa e geral.
Mais fácil é descrever aspectos que se relacionam à energia e que, individualmente e como um todo, nos ajudam a ter uma compreensão cada vez melhor do seu significado.
Vejamos, a seguir, alguns aspectos básicos para a compreensão do conceito de energia.
1) A quantidade que chamamos energia pode ocorrer em diversas formas. Energia pode ser transformada, ou convertida, de uma forma em outra (conversão de energia).
Exemplo:
A energia mecânica de uma queda d’água é convertida em energia elétrica a qual, por exemplo, é utilizada para estabilizar a temperatura de um aquário (conversão em calor) aumentando, com isso, a energia interna do sistema em relação à que teria à temperatura ambiente. As moléculas do meio, por sua vez, recebem do aquário energia que causa um aumento em sua energia cinética de rotação e translação.
2) Cada corpo e igualmente cada “sistema” de corpos contém energia. Energia pode ser transferida de um sistema para outro (transferência de energia).
Exemplo:
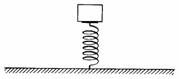
Um sistema massa/mola é mantido em repouso com a mola distendida. Nestas condições, ele armazena energia potencial. Quando o sistema é solto, ele oscila durante um determinado tempo mas acaba parando. A energia mecânica que o sistema possuía inicialmente acaba transferida para o meio que o circunda (ar) na forma de um aumento da energia cinética de translação e rotação das moléculas do ar.
3) Quando energia é transferida de um sistema para outro, ou quando ela é convertida de uma forma em outra, a quantidade de energia não muda (conservação de energia).
Exemplo:
A energia cinética de um automóvel que pára é igual à soma das diversas formas de energia nas quais ela se converte durante o acionamento do sistema de freios que detém o carro por atrito nas rodas.
4) Na conversão, a energia pode transformar-se em energia de menor qualidade, não aproveitável para o consumo. Por isso, há necessidade de produção de energia apesar da lei de conservação. Dizemos que a energia se degrada (degradação de energia).
Exemplo:
Em nenhum dos três exemplos anteriores, a energia pode “refluir” e assumir sua condição inicial. Nunca se viu automóvel arrancar reutilizando a energia convertida devido ao acionamento dos freios quando parou. Ela se degradou. Daí resulta a necessidade de produção constante (e crescente) de energia.

Considerações Gerais
|
C |
hamamos de Energia Mecânica a todas as formas de energia relacionadas com o movimento de corpos ou com a capacidade de colocá-los em movimento ou deformá-los.
Classes de energia mecânica
1) Energia potencial
É a que tem um corpo que, em virtude de sua posição ou estado, é capaz de realizar trabalho.[3]
Podemos classificar a energia potencial em:
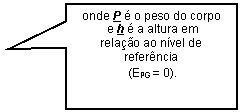
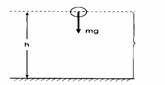
a) Energia Potencial Gravitacional (EPG)
Está relacionada com a posição que um corpo ocupa no campo gravitacional terrestre e sua capacidade de vir a realizar trabalho mecânico.
Matematicamente
|
|
|
|||||
|
Ou, sabendo que P = m.g,
|
||||||
Exercícios resolvidos:
1) Um corpo de massa 4 kg encontra-se a uma altura de 16 m do solo. Admitindo o solo como nível de referência e supondo g = 10 m/s2, calcular sua energia potencial gravitacional.
Resolução:
![]() è
è ![]() è
è![]()
![]()
![]()
2) Um corpo de massa 40 kg tem energia potencial gravitacional de 800J em relação ao solo. Dado g = 10 m/s2 , calcule a que altura se encontra do solo.
Resolução:
![]() è
è![]() è
è![]() è
è![]()
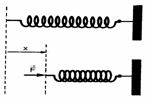
b) Energia Potencial Elástica (EPE)
É a energia armazenada em uma mola comprimida ou distendida.
Matematicamente
|
|
|
Exercícios resolvidos:
3) Uma mola de constante elástica k = 400 N/m é comprimida de 5 cm. Determinar a sua energia potencial elástica.
Resolução:![]() è
è![]() è
è![]()
4) Qual é a distensão de uma mola de constante elástica k = 100 N/m e que está armazenando uma energia potencial elástica de 2J?
Resolução:![]() è
è![]() è
è![]() è
è![]()
2) Energia Cinética (EC)
Todo corpo em movimento possui uma energia associada a esse movimento que pode vir a realizar um trabalho (em uma colisão por exemplo). A essa energia damos o nome de energia cinética.
Matematicamente
 |
Exercícios resolvidos:
5) Determine a energia cinética de um móvel de massa 50 kg e velocidade 20 m/s.
Resolução:
![]() è
è![]() è
è![]()
![]()
U |
ma força é chamada conservativa, quando pode devolver o trabalho realizado para vencê-la. Desse modo, o peso de um corpo e a força elástica são exemplos desse tipo de força. No entanto, a força de atrito cinético, que não pode devolver o trabalho realizado para vencê-la, é uma força não-conservativa, ou dissipativa (ocorre degradação da energia mecânica).
Isso quer dizer que, em um sistema no qual só atuam forças conservativas (sistema conservativo), a ENERGIA MECÂNICA (EM) se conserva, isto é, mantém-se com o mesmo valor em qualquer momento, mas alternando-se nas suas formas cinética e potencial (gravitacional ou elástica).
 |
Exercícios resolvidos:
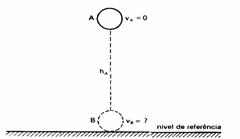
6) Uma esfera de massa 5 kg é abandonada de uma altura de 45m num local onde g = 10 m/s2. Calcular a velocidade do corpo ao atingir o solo. Despreze os efeitos do ar.
Resolução:
Desprezando a resistência do ar, o sistema é conservativo, logo:
|
|
|
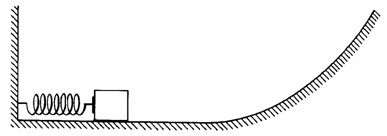
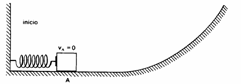
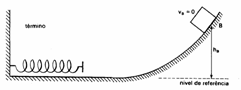
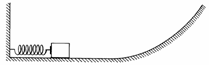
7) Um corpo de 2 kg é empurrado contra uma mola de constante elástica 500 N/m, comprimindo-a 20 cm.
Ele é libertado e a mola o projeta ao longo de uma superfície lisa e horizontal que termina numa rampa inclinada conforme indica a figura. Dado g = 10 m/s2 e desprezando todas as formas de atrito, calcular a altura máxima atingida pelo corpo na rampa.
|
|
 Resolução:
Resolução:
 |
|
|
|
Como o sistema é conservativo, temos:
![]() è
è ![]()
![]()
![]()
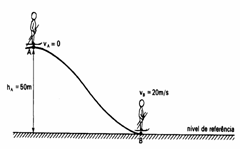
![]()
8) Um esquiador de massa 60 kg desliza de uma encosta, partindo do repouso, de uma altura de 50 m. Sabendo que sua velocidade ao chegar no fim da encosta é de 20 m/s, calcule a perda de energia mecânica devido ao atrito. Adote g = 10 m/s2.
Resolução:
|
|
|
Exercícios propostos:
|
1) Um garoto abandona uma pedra de massa 20 g do alto de um viaduto de 5 m de altura em relação ao solo. Considerando g = 10 m/s2 , determine a velocidade e a energia cinética da pedra ao atingir o solo. (Despreze os efeitos do ar.)
|
Resolução: |
|||
|
2) Um corpo de massa 0,5 kg é lançado, do solo, verticalmente para cima com velocidade de 12 m/s. Desprezando a resistência do ar e adotando g = 10 m/s2, calcule a altura máxima, em relação ao solo, que o corpo alcança.
|
Resolução: |
|||
|
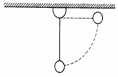
3) Um pêndulo de massa 1 kg é levado a posição horizontal e então abandonado. |
|
Resolução: |
||
|
Sabendo que o fio tem um comprimento de 0,8 m e g = 10 m/s2, calcule a velocidade do pêndulo quando passar pela posição de altura mínima. |
||||
|
4) Do alto de uma torre de 61,6 n de altura, lança-se verticalmente para baixo, um corpo com velocidade de 8 m/s. Calcule a velocidade com que o corpo atinge o solo. Adote g = 10 m/s2 e despreze os efeitos do ar. |
Resolução:
|
|||
|
5) Um corpo de massa 2 kg é lançado do solo, verticalmente para cima, com velocidade de 50 m/s. Sabendo que, devido ao atrito com o ar, o corpo dissipa 100 J de energia sob a forma de calor, determine a altura máxima atingida pelo corpo. Adote g = 10 m/s2. |
Resolução: |
|||
|
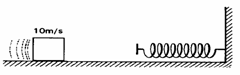
6) Um corpo de massa igual a 0,5 kg e velocidade constante de 10 m/s choca-se com uma mola de constante elástica 800n/s. Desprezando os atritos, calcule a máxima deformação sofrida pela. mola.
|
Resolução:
|
|||
|
7) Consideremos uma mola de constante elástica 400 N/m, e um corpo de massa 1 kg nela encostado que produz uma compressão de 0,8 m. Liberando a mola, qual é a velocidade do corpo no instante em que perde contato com ela? Despreze as forças de resistência.
|
Resolução: |
|||
|
8) No escorregador mostrado na figura, uma criança com 30 kg de massa, partindo do repouso em A, desliza até B. |
|
Resolução: |
||
|
Desprezando as perdas de energia e admitindo g = 10 m/s2, calcule a velocidade da criança ao chegar a B.
|
||||
|
9) Um corpo de massa m é empurrado contra uma mola cuja constante elástica é 600 N/s, comprimindo-a 30 cm. Ele é liberado e a mola o projeta ao longo de uma superfície sem atrito que termina numa rampa inclinada conforme a figura. Sabendo que a altura máxima atingida pelo corpo na rampa é de 0,9 m e g = 10 m/s2, calcule m. (Despreze as forças resistivas.)
|
Resolução: |
|||
|
10) Um corpo de massa 20 kg está sobre uma mola comprimida de 40 cm. Solta-se a mola e deseja-se que o corpo atinja a altura de 10 m em relação à sua posição inicial. |
|
Resolução: |
||
|
Determine a constante elástica da mola. Adote g = 10 m/s2 e despreze os efeitos do ar. |
||||
|
11) Uma esfera parte do repouso em A e percorre o caminho representado sem nenhum atrito ou resistência. Determine sua velocidade no ponto B.
|
Resolução: |
|||
|
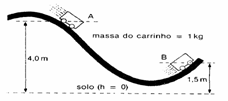
12) Um carrinho situado no ponto (veja a figura), parte do repouso e alcança o ponto B. a) Calcule a velocidade do carrinho em B, sabendo que 50% de sua energia mecânica inicial é dissipada pelo atrito no trajeto. b) Qual foi o trabalho do atrito entre A e B?
|
Resolução: |
|||
|
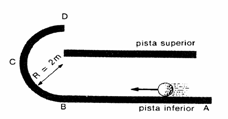
13) Uma esfera de massa 2 kg é lançada horizontalmente do ponto A e deseja-se que ela atinja a pista superior. Os trechos AB e BCD são perfeitamente lisos. A aceleração da gravidade é de 10 m/s2. Determine a mínima velocidade que o corpo deve ter ao atingir o ponto B.
|
Resolução: |
|||
|
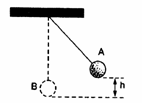
14) Uma esfera é suspensa por um fio ideal. Quando abandonada da posição A sem velocidade inicial, ela passa por B com velocidade de 10 m/s. Desprezando as resistências, determine o valor da altura h, de onde a esfera foi solta. Adote g = 10 m/s2.
|
Resolução: |
|||

1) 10 m/s
2) 7,2 m/s
3) 4 m/s
4) 36 m/s
5) 120 m
6) 0,25 m
7) 1,6 m/s
8) 8 m/s
9) 3 kg
10) 25 N/m
11) 10 m/s
12) ![]() e –20J
e –20J
13) 10 m/s
14) 5 m